Generalized Trigonometric Functions

$$$$

This page documents how trigonometric functions generalize to elliptical trigonometry and hyperbolic trigonometry.

Preliminaries

Recall the power series expansions of the conventional trigonometric functions and their inverses.

Trigonometric Functions

For the conventional trigonometric functions, we have the following series:

$$\begin{array}{rlrlrlrlrlrlrlrlrlrl}{e}^x& =\sum _{n=0}^{\mathrm{\infty }}\frac{x^n}{n!}& & =1& & +x& & +\frac{x^2}{2!}& & +\frac{x^3}{3!}& & +\frac{x^4}{4!}& & +\frac{x^5}{5!}& & +\frac{x^6}{6!}& & +\frac{x^7}{7!}& & +\cdots \\ \\ \cos (x)& =\sum _{n=0}^{\mathrm{\infty }}(-1{)}^n\frac{x^{2n}}{(2n)!}& & =1& & & & -\frac{x^2}{2!}& & & & +\frac{x^4}{4!}& & & & -\frac{x^6}{6!}& & & & +\cdots \\ \sin (x)& =\sum _{n=0}^{\mathrm{\infty }}(-1{)}^n\frac{x^{2n+1}}{(2n+1)!}& & =& & +x& & & & -\frac{x^3}{3!}& & & & +\frac{x^5}{5!}& & & & -\frac{x^7}{7!}& & +\cdots \\ \\ \cosh (x)& =\sum _{n=0}^{\mathrm{\infty }}(+1{)}^n\frac{x^{2n}}{(2n)!}& & =1& & & & +\frac{x^2}{2!}& & & & +\frac{x^4}{4!}& & & & +\frac{x^6}{6!}& & & & +\cdots \\ \sinh (x)& =\sum _{n=0}^{\mathrm{\infty }}(+1{)}^n\frac{x^{2n+1}}{(2n+1)!}& & =& & +x& & & & +\frac{x^3}{3!}& & & & +\frac{x^5}{5!}& & & & +\frac{x^7}{7!}& & +\cdots \end{array}$$

In particular, note how the series for $\cos$/$\cosh$ contain all the $even$ powers and for $\sin$/$\sinh$ contain all the $odd$ powers.

For example, it follows directly that:

$$e^x=\cosh (x)+\sinh (x)$$

And also:

$$\begin{array}{rl}\cosh (x)& =\frac{1}{2}(e^x+e^{-x})\\ \\ \sinh (x)& =\frac{1}{2}(e^x-e^{-x})\end{array}$$

Inverse Trigonometric Functions

Furthermore, we have the following series, which converge for for $|x|<1$:

$$\begin{array}{rlrlrlrlrlrlrlrlrl}\log (1+x)& =\sum _{n=0}^{\mathrm{\infty }}(-1{)}^n\frac{x^{n+1}}{n+1}& & =x& & -\frac{x^2}{2}& & +\frac{x^3}{3}& & -\frac{x^4}{4}& & +\frac{x^5}{5}& & -\frac{x^6}{6}& & +\frac{x^7}{7}& & +\cdots \\ \\ {\tan }^{-1}(x)& =\sum _{n=0}^{\mathrm{\infty }}(-1{)}^n\frac{x^{2n+1}}{2n+1}& & =x& & & & -\frac{x^3}{3}& & & & +\frac{x^5}{5}& & & & -\frac{x^7}{7}& & +\cdots \\ \\ {\tanh }^{-1}(x)& =\sum _{n=0}^{\mathrm{\infty }}(+1{)}^n\frac{x^{2n+1}}{2n+1}& & =x& & & & +\frac{x^3}{3}& & & & +\frac{x^5}{5}& & & & +\frac{x^7}{7}& & +\cdots \end{array}$$

For example, it follows directly that:

$${\tanh }^{-1}(x)=\frac{1}{2}(\log (1+x)-\log (1-x))$$

Generalization

Definitions

The power series above suggest a possible generalization:

$$\begin{array}{rlrlrlrlrlrlrlrlrlrl}{\mathfrak{c}}_{\mathrm{k}}(x)& =\sum _{n=0}^{\mathrm{\infty }}(-k{)}^n\frac{x^{2n}}{(2n)!}& & =1& & & & -k\frac{x^2}{2!}& & & & +k^2\frac{x^4}{4!}& & & & -k^3\frac{x^6}{6!}& & & & +\cdots \\ {\mathfrak{s}}_{\mathrm{k}}(x)& =\sum _{n=0}^{\mathrm{\infty }}(-k{)}^n\frac{x^{2n+1}}{(2n+1)!}& & =& & +x& & & & -k\frac{x^3}{3!}& & & & +k^2\frac{x^5}{5!}& & & & -k^3\frac{x^7}{7!}& & +\cdots \end{array}$$

Note that from these power series, it follows immediately:

$$\begin{array}{rl}{\mathfrak{c}}_{+1}(x)& =\cos (x)\\ {\mathfrak{s}}_{+1}(x)& =\sin (x)\\ \\ {\mathfrak{c}}_0(x)& =1\\ {\mathfrak{s}}_0(x)& =x\\ \\ {\mathfrak{c}}_{-1}(x)& =\cosh (x)\\ {\mathfrak{s}}_{-1}(x)& =\sinh (x)\end{array}$$

As in conventional trigonometry, we can define the tangent function as:

$${\mathfrak{t}}_{\mathrm{k}}(x)=\frac{{\mathfrak{s}}_{\mathrm{k}}(x)}{{\mathfrak{c}}_{\mathrm{k}}(x)}$$

The power series are sufficient to define ${\mathfrak{c}}_{\mathrm{k}}$ and ${\mathfrak{s}}_{\mathrm{k}}$. However, in practice, for numerical computation it is convenient to define these functions in terms of the commonly available trigonometric functions:

$$\begin{array}{rl}{\mathfrak{c}}_{\mathrm{k}}(x)& =\{\begin{array}{ll}\cos (\sqrt{k}x)& \text{if }k>0,\\ 1& \text{if }k=0,\\ \cosh (\sqrt{-k}x)& \text{if }k<0.\end{array}\\ \\ {\mathfrak{s}}_{\mathrm{k}}(x)& =\{\begin{array}{ll}\frac{1}{\sqrt{k}}\sin (\sqrt{k}x)& \text{if }k>0,\\ x& \text{if }k=0,\\ \frac{1}{\sqrt{-k}}\sinh (\sqrt{-k}x)& \text{if }k<0.\end{array}\\ \\ {\mathfrak{t}}_{\mathrm{k}}(x)& =\{\begin{array}{ll}\frac{1}{\sqrt{k}}\tan (\sqrt{k}x)& \text{if }k>0,\\ x& \text{if }k=0,\\ \frac{1}{\sqrt{-k}}\tanh (\sqrt{-k}x)& \text{if }k<0.\end{array}\end{array}$$

The inverses of ${\mathfrak{c}}_{\mathrm{k}}$, ${\mathfrak{s}}_{\mathrm{k}}$, and ${\mathfrak{t}}_{\mathrm{k}}$ can be computed as follows:

$$\begin{array}{rl}{{\mathfrak{c}}_{\mathrm{k}}}^{-1}(x)& =\{\begin{array}{ll}\frac{1}{\sqrt{k}}{\cos }^{-1}(x)& \text{if }k>0,\\ \text{undefined}& \text{if }k=0,\\ \frac{1}{\sqrt{-k}}{\cosh }^{-1}(x)& \text{if }k<0.\end{array}\\ \\ {{\mathfrak{s}}_{\mathrm{k}}}^{-1}(x)& =\{\begin{array}{ll}\frac{1}{\sqrt{k}}{\sin }^{-1}(\sqrt{k}x)& \text{if }k>0,\\ x& \text{if }k=0,\\ \frac{1}{\sqrt{-k}}{\sinh }^{-1}(\sqrt{-k}x)& \text{if }k<0.\end{array}\\ \\ {{\mathfrak{t}}_{\mathrm{k}}}^{-1}(x)& =\{\begin{array}{ll}\frac{1}{\sqrt{k}}{\tan }^{-1}(\sqrt{k}x)& \text{if }k>0,\\ x& \text{if }k=0,\\ \frac{1}{\sqrt{-k}}{\tanh }^{-1}(\sqrt{-k}x)& \text{if }k<0.\end{array}\end{array}$$

(Note: I first encountered these formulations in McRae.)

Identities

The generalized functions obey the following generalized "Pythagorean" identity:

$${\mathfrak{c}}_{\mathrm{k}}(x{)}^2+k{\mathfrak{s}}_{\mathrm{k}}(x{)}^2=1$$

The following angle addition/subtraction identities hold:

$$\begin{array}{rl}{\mathfrak{c}}_{\mathrm{k}}(x\pm y)& ={\mathfrak{c}}_{\mathrm{k}}(x){\mathfrak{c}}_{\mathrm{k}}(y)\mp k{\mathfrak{s}}_{\mathrm{k}}(x){\mathfrak{s}}_{\mathrm{k}}(y)\\ \\ {\mathfrak{s}}_{\mathrm{k}}(x\pm y)& ={\mathfrak{s}}_{\mathrm{k}}(x){\mathfrak{c}}_{\mathrm{k}}(y)\pm {\mathfrak{c}}_{\mathrm{k}}(x){\mathfrak{s}}_{\mathrm{k}}(y)\\ \\ {\mathfrak{t}}_{\mathrm{k}}(x\pm y)& =\frac{{\mathfrak{s}}_{\mathrm{k}}(x){\mathfrak{c}}_{\mathrm{k}}(y)\pm {\mathfrak{c}}_{\mathrm{k}}(x){\mathfrak{s}}_{\mathrm{k}}(y)}{{\mathfrak{c}}_{\mathrm{k}}(x){\mathfrak{c}}_{\mathrm{k}}(y)\mp k{\mathfrak{s}}_{\mathrm{k}}(x){\mathfrak{s}}_{\mathrm{k}}(y)}=\frac{{\mathfrak{t}}_{\mathrm{k}}(x)\pm {\mathfrak{t}}_{\mathrm{k}}(y)}{1\mp k{\mathfrak{t}}_{\mathrm{k}}(x){\mathfrak{t}}_{\mathrm{k}}(y)}\end{array}$$

The following angle multiplication/division identities hold:

$$\begin{array}{rl}{\mathfrak{c}}_{\mathrm{k}}(xy)& ={\mathfrak{c}}_{{\mathrm{kx}}^2}(y)={\mathfrak{c}}_{{\mathrm{ky}}^2}(x)\\ \\ {\mathfrak{s}}_{\mathrm{k}}(xy)& =x{\mathfrak{s}}_{{\mathrm{kx}}^2}(y)=y{\mathfrak{s}}_{{\mathrm{ky}}^2}(x)\\ \\ {\mathfrak{t}}_{\mathrm{k}}(xy)& =x{\mathfrak{t}}_{{\mathrm{kx}}^2}(y)=y{\mathfrak{t}}_{{\mathrm{ky}}^2}(x)\end{array}$$

As special cases of the above, we have:

$$\begin{array}{rl}{\mathfrak{c}}_{\mathrm{k}}(x)& ={\mathfrak{c}}_{{\mathrm{kx}}^2}(1)\\ \\ {\mathfrak{s}}_{\mathrm{k}}(x)& =x{\mathfrak{s}}_{{\mathrm{kx}}^2}(1)\\ \\ {\mathfrak{t}}_{\mathrm{k}}(x)& =x{\mathfrak{t}}_{{\mathrm{kx}}^2}(1)\end{array}$$

Derivatives

The derivatives of ${\mathfrak{c}}_{\mathrm{k}}$, ${\mathfrak{s}}_{\mathrm{k}}$, and ${\mathfrak{t}}_{\mathrm{k}}$ are as follows:

$$\begin{array}{rl}{{\mathfrak{c}}_{\mathrm{k}}}^{\prime }(x)& =-k{\mathfrak{s}}_{\mathrm{k}}(x)\\ \\ {{\mathfrak{s}}_{\mathrm{k}}}^{\prime }(x)& ={\mathfrak{c}}_{\mathrm{k}}(x)\\ \\ {{\mathfrak{t}}_{\mathrm{k}}}^{\prime }(x)& =1+k{\mathfrak{t}}_{\mathrm{k}}(x{)}^2\end{array}$$

Plots

By plotting ${\mathfrak{c}}_{\mathrm{k}}$ for varying values of $k$ we obtain:

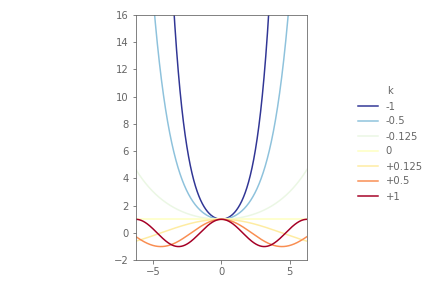
By plotting ${\mathfrak{s}}_{\mathrm{k}}$ for varying values of $k$ we obtain:

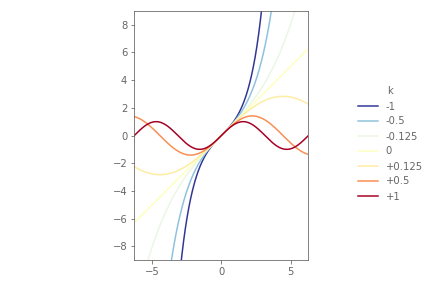
By plotting ${\mathfrak{t}}_k$ for varying values of $k$ we obtain:

Polar Coordinates

Let us consider the following parametric equation:

$$\left(\begin{array}{c}x\\ y\end{array}\right)=\left(\begin{array}{c}r{\mathfrak{c}}_{\mathrm{k}}(\theta )\\ r{\mathfrak{s}}_{\mathrm{k}}(\theta )\end{array}\right)$$

With the aid of the generalized "Pythagorean" identity we can derive the implicit form by eliminating $\theta$:

$$x^2+k{y}^2=r^2$$

By setting $r^2=1$ and plotting this equation for varying values of $k$ we obtain:

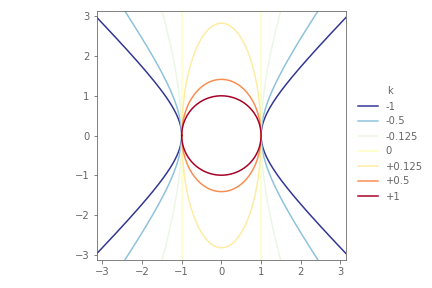
As can be seen in the plot, resulting shapes are:

• Ellipses for $k>0$
• Paralell Line Pair for $k=0$
• Hyperbolas for $k<0$

Demos

Angles

The demo below illustrates the generalized concept of angles for varying values of $k$.

k = 1θ = 0.78

Polar Coordinates

The demo below shows the real (solid) and imaginary (dashed) unit circles for varying values of $k$ along with a point specified in polar coordinates.

k = 1r = 1θ = 0

References

• McRae
• Hammack