n-Plex Numbers
$$ \newcommand{\lmat}[1]{\mathbf{X}({#1})} \newcommand{\rmat}[1]{\mathbf{Y}({#1})} \newcommand{\conj}[1]{\overline{#1}} \newcommand{\conjs}[2]{ {^{^{#1}}\overline{#2}} } \newcommand{\V}[1]{\mathbf{#1}} \newcommand{\M}[1]{\mathbf{#1}} \newcommand{\I}[1]{#1} \newcommand{\K}[1]{#1} \newcommand{\A}[1]{\mathbf{#1}} \newcommand{\scalars}[2][]{\K{#2}\I{#1}} \newcommand{\versors}[2][]{\A{#2}\I{#1}} \newcommand{\us}[1]{\scalars[^{#1}]{u}} \newcommand{\vs}[1]{\scalars[^{#1}]{v}} \newcommand{\ws}[1]{\scalars[^{#1}]{w}} \newcommand{\xs}[1]{\scalars[^{#1}]{x}} \newcommand{\ys}[1]{\scalars[^{#1}]{y}} \newcommand{\zs}[1]{\scalars[^{#1}]{z}} \newcommand{\es}[1]{\versors[_{#1}]{e}} \newcommand{\fs}[1]{\versors[_{#1}]{f}} \newcommand{\Xs}[2]{\scalars[_{#1}^{#2}]{X}} \newcommand{\Ys}[2]{\scalars[_{#1}^{#2}]{Y}} \newcommand{\Zs}[2]{\scalars[_{#1}^{#2}]{Z}} \newcommand{\Cs}[3]{\scalars[_{#1#2}^{#3}]{C}} $$This exploration was inspired by the YouTube video "Let's Invent the Triplex Numbers". In the following we will generalize the construction used for the triplex numbers to arbitrary dimensions.
It started out as an excercise to build a better understanding of algebraic structures by worked examples. However, it turns out that the generalization has some rather nice structure and connections to other areas of mathematics. I am fairly certain most of these things are well known, however I have not seen them presented in this particular way.
Preliminaries
This page makes use of various concepts from hypercomplex numbers.
Roots of Unity
An $n$-th root of unity, is a number z satisfying the equation:
$$ z^{n} = 1 $$
In the following, we use $\zeta^{k}$ to denote the $n$-th roots of unity.
$$ \zeta^{k} = e^{2\pi i \frac{k}{n}} $$
A useful way of thinking about $\zeta^{k}$ is as a $\frac{k}{n}$-th turn counter-clockwise and the complex conjugate $\bar{\zeta}^{k}$ as a $\frac{k}{n}$-th turn clockwise around the unit circle. Below is a plot of the 5-th roots of unity:

Eigenvalue Decomposition
In order to obtain diagonal bases for the $n$-plex numbers we use the eigenvalue decomposition.
Definitions
The $n$-plex numbers $Pl_{n}(\mathbb{K})$ can be understood as an algebra over a field $\mathbb{K}$ with the cyclic group of order $n$ as its basis. To build intuition, I will first go through the construction of the $n$-plex numbers for several small $n$, before presenting the fully general construction.
2-Plex Numbers
Our starting point are the 2-plex numbers $Pl_{2}(\mathbb{R})$, which correspond to the split-complex numbers $\mathbb{R}[\A{j}] / (j^{2} - 1)$.
$$ Pl_{2} \cong \mathbb{R}[\A{j}] / (j^{2} - 1) \cong \mathbb{R} \oplus \mathbb{R} $$
Standard Basis
The 2-plex number $\A{x}$ can be written in the standard basis as:
$$ \A{x} = \es{0}\xs{0} + \es{1}\xs{1} $$
Multiplication
The construction is as follows:
$$ \begin{align*} \left(\es{1}\right)^0 &= \es{0} \\ \left(\es{1}\right)^1 &= \es{1} \\ \left(\es{1}\right)^2 &= \es{0} \\ &\vdots \\ \end{align*} $$Resulting in the multiplication table:
Which gives the multiplication operation:
$$ \A{x}\A{y} = \left(\es{0}\xs{0} + \es{1}\xs{1}\right)\left(\es{0}\ys{0} + \es{1}\ys{1}\right) = \es{0}\left(\xs{0}\ys{0} + \xs{1}\ys{1}\right) + \es{1}\left(\xs{1}\ys{0} + \xs{0}\ys{1}\right) $$
The multiplicative unit is:
$$ \A{1} = \es{0} $$
Conjugate and Quadratic Form
The 2-plex number $\A{x}$ has the following principal conjugations:
$$ \begin{align*} \conjs{0}{\A{x}} &= \es{0}\xs{0} + \es{1}\xs{1} \\ \conjs{1}{\A{x}} &= \es{0}\xs{0} - \es{1}\xs{1} \\ \end{align*} $$
The resulting conjugate is:
$$ \conj{\A{x}} = \conjs{1}{\A{x}} = \es{0}\xs{0} - \es{1}\xs{1} $$
The resulting quadratic form is:
$$ N(\A{x}) = \A{x}\conj{\A{x}} = \A{1}\left(\left(\xs{0}\right)^{2} - \left(\xs{1}\right)^{2}\right) $$
Plotting all $\A{x}$ with $N(\A{x}) = +1, 0, -1$ we obtain:
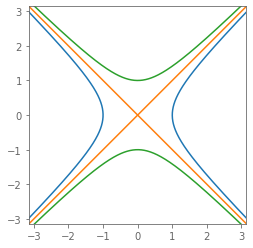
The multiplicative inverse when $N(\A{x}) \ne 0$ is:
$$\A{x}^{-1} = \frac{\conj{\A{x}}}{N(\A{x})}$$
Matrix Representation
The $2$-plex number $\A{x}$ in standard basis has the following matrix representation:
We can verify that this corresponds to the expected multiplication:
Diagonal Basis
The 2-plex number $\A{u}$ can be written in the diagonal basis as:
$$ \A{u} = \fs{0}\us{0} + \fs{1}\us{1} $$
Multiplication
The construction is as follows:
$$ \begin{align*} \fs{0} &= \frac{1}{2} (\es{0} + \es{1}) \\ \fs{1} &= \frac{1}{2} (\es{0} - \es{1}) \\ \end{align*} $$Resulting in the multiplication table:
Which gives the multiplication operation:
$$ \A{u}\A{v} = \left(\fs{0}\us{0} + \fs{1}\us{1}\right)\left(\fs{0}\vs{0} + \fs{1}\vs{1}\right) = \fs{0}\left(\us{0}\vs{0}\right) + \fs{1}\left(\us{1}\vs{1}\right) $$
The multiplicative unit is:
$$ \A{1} = \fs{0} + \fs{1} $$
Conjugate and Quadratic Form
The 2-plex number $\A{u}$ has the following principal conjugations:
$$ \begin{align*} \conjs{0}{\A{u}} &= \fs{0}\us{0} + \fs{1}\us{1} \\ \conjs{1}{\A{u}} &= \fs{0}\us{1} + \fs{1}\us{0} \\ \end{align*} $$The resulting conjugate is:
$$ \conj{\A{u}} = \conjs{1}{\A{u}} = \fs{0}\us{1} + \fs{1}\us{0} $$
The resulting quadratic form is:
$$ N(\A{u}) = \A{u}\conj{\A{u}} = \A{1}\left(\us{0}\us{1}\right) $$
The multiplicative inverse when $N(\A{x}) \ne 0$ is:
$$\A{x}^{-1} = \frac{\conj{\A{x}}}{N(\A{x})}$$
Matrix Representation
The $2$-plex number $\A{u}$ in diagonal basis has the following matrix representation:
We can verify that this corresponds to the expected multiplication:
Basis Conversion
The matrix representation $\A{X}(\A{x})$ admits the following decomposition:
$$ \begin{align*} \lmat{\A{x}} &= \A{P} \, \A{D}(\A{x}) \, \A{P}^{-1} \\ \\ \lmat{\A{x}} &= \begin{bmatrix} \xs{0} & \xs{1} \\ \xs{1} & \xs{0} \\ \end{bmatrix}\\ \\ \A{D}(\A{x}) &= \begin{bmatrix} \xs{0} + \xs{1} & 0 \\ 0 & \xs{0} - \xs{1} \\ \end{bmatrix}\\ \\ \A{P} &= \begin{bmatrix} 1 & 1 \\ 1 & -1 \\ \end{bmatrix}\\ \end{align*} $$Consequently, it is possible to use $\A{P}$ to convert between standard and diagonal basis.
A 2-plex number $\A{x}$ in standard basis can be written in diagonal basis as:
$$ \A{x} = \es{0}\xs{0} + \es{1}\xs{1} = \fs{0}(\xs{0}+\xs{1}) + \fs{1}(\xs{0}-\xs{1}) $$
A 2-plex number $\A{u}$ in diagonal basis can be written in standard basis as:
$$ \A{u} = \fs{0}\us{0} + \fs{1}\us{1} = \es{0}\frac{1}{2}(\us{0}+\us{1}) + \es{1}\frac{1}{2}(\us{0}-\us{1}) $$
3-Plex Numbers
We move on to the 3-plex numbers $Pl_{3}(\mathbb{R})$, which correspond to the triplex numbers covered in the video.
$$ Pl_{3} \cong \mathbb{R} \oplus \mathbb{C} $$
Standard Basis
The 3-plex number $\A{x}$ can be written in the standard basis as:
$$ \A{x} = \es{0}\xs{0} + \es{1}\xs{1} + \es{2}\xs{2} $$
Multiplication
The construction is as follows:
$$ \begin{align*} \left(\es{1}\right)^0 &= \es{0}\\ \left(\es{1}\right)^1 &= \es{1}\\ \left(\es{1}\right)^2 &= \es{2}\\ \left(\es{1}\right)^3 &= \es{0}\\ &\vdots \\ \end{align*} $$
Resulting in the multiplication table:
Which gives the multiplication operation:
$$ \begin{alignat}{2} \A{x}\A{y} &={} &&\left(\es{0}\xs{0} + \es{1}\xs{1} + \es{2}\xs{2}\right)\left(\es{0}\ys{0} + \es{1}\ys{1} + \es{2}\ys{2}\right) \\ &= && \es{0}\left(\xs{0}~ \ys{0}+ \xs{2}~ \ys{1}+ \xs{1}~ \ys{2}\right) + \\ & && \es{1}\left(\xs{1}~ \ys{0}+ \xs{0}~ \ys{1}+ \xs{2}~ \ys{2}\right) + \\ & && \es{2}\left(\xs{2}~ \ys{0}+ \xs{1}~ \ys{1}+ \xs{0}~ \ys{2}\right) \end{alignat} $$
The multiplicative unit is:
$$ \A{1} = \es{0} $$
Conjugate and Cubic Form
The 3-plex number $\A{x}$ has the following principal conjugations:
$$ \begin{align*} \conjs{0}{\A{x}} &= \es{0}\xs{0} + \es{1}\xs{1} + \es{2}\xs{2} \\ \conjs{1}{\A{x}} &= \es{0}\xs{0} - \es{1}\frac{1}{2}\left(1-\sqrt{3}i\right) - \es{2}\frac{1}{2}\left(1+\sqrt{3}i\right) \\ \conjs{2}{\A{x}} &= \es{0}\xs{0} - \es{1}\frac{1}{2}\left(1+\sqrt{3}i\right) - \es{2}\frac{1}{2}\left(1-\sqrt{3}i\right) \\ \end{align*} $$
The resulting conjugate is:
$$ \conj{\A{x}} = \conjs{1}{\A{x}} \; \conjs{2}{\A{x}} = \es{0}\left(\left(\xs{0}\right)^{2} - \xs{1}\xs{2}\right) + \es{1}\left(\left(\xs{2}\right)^{2} - \xs{0}\xs{1}\right) + \es{2}\left(\left(\xs{1}\right)^{2} - \xs{0}\xs{2}\right) $$
The resulting cubic form is:
$$ N(\A{x}) = \A{x}\conj{\A{x}} = \A{1}\left(\left(x^{0}\right)^{3} + \left(x^{1}\right)^{3} + \left(x^{2}\right)^{3} - 3 x^{0} x^{1} x^{2} \right) $$
Plotting all $\A{x}$ with $N(\A{x}) = +1, 0, -1$ we obtain:
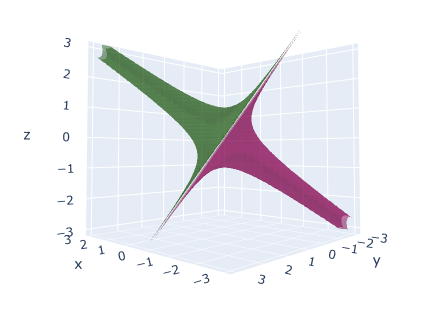
The multiplicative inverse when $N(\A{x}) \ne 0$ is:
$$\A{x}^{-1} = \frac{\conj{\A{x}}}{N(\A{x})}$$
Matrix Representation
The $3$-plex number $\A{x}$ has the following matrix representation:
We can verify that this corresponds to the expected multiplication:
Diagonal Basis
The 3-plex number $\A{u}$ can be written in the diagonal basis as:
$$ \A{u} = \fs{0}\us{0} + \fs{1}\us{1} + \fs{2}\us{2} $$
Multiplication
The construction is as follows:
$$ \begin{align*} \fs{0} &= \frac{1}{3} (\es{0} + \es{1} + \es{2}) \\ \fs{1} &= \frac{1}{3} (2\es{0} - \es{1} - \es{2}) \\ \fs{2} &= -\frac{1}{\sqrt{3}} (\es{1} - \es{2}) \\ \end{align*} $$Resulting in the multiplication table:
Which gives the multiplication operation:
$$ \begin{alignat}{2} \A{u}\A{v} &={} &&\left(\fs{0}\us{0} + \fs{1}\us{1} + \fs{2}\us{2}\right)\left(\fs{0}\vs{0} + \fs{1}\vs{1} + \fs{2}\vs{2}\right) \\ &= && \fs{0}\left(\us{0}~ \vs{0}\right) + \\ & && \fs{1}\left(\us{1}~ \vs{1}- \us{2}~ \vs{2}\right) + \\ & && \fs{2}\left(\us{2}~ \vs{1}+ \us{1}~ \vs{2}\right) \end{alignat} $$
The multiplicative unit is:
$$ \A{1} = \fs{0} + \fs{1} $$
Conjugate and Quadratic Form
The $3$-plex number $\A{u}$ has the following principal conjugations:
$$ \begin{align*} \conjs{0}{\A{u}} &= \fs{0}\us{0} + \fs{1}\us{1} + \fs{2}\us{2} \\ \conjs{1}{\A{u}} &= \fs{0}\left(\us{1} + i\us{2}\right) + \fs{1}\frac{1}{2}\left(\us{0} + \us{1} - i\us{2}\right) + \fs{2}\frac{i}{2}\left(\us{0} - \us{1} + i\us{2}\right) \\ \conjs{2}{\A{u}} &= \fs{0}\left(\us{1} - i\us{2}\right) + \fs{1}\frac{1}{2}\left(\us{0} + \us{1} + i\us{2}\right) - \fs{2}\frac{i}{2}\left(\us{0} - \us{1} - i\us{2}\right) \\ \end{align*} $$The resulting conjugate is:
$$ \conj{\A{u}} = \conjs{1}{\A{u}} \; \conjs{2}{\A{u}} = \fs{0}\left(\left(\us{1}\right)^{2} + \left(\us{2}\right)^{2}\right) + \fs{1}\left(\us{0}\us{1}\right) - \fs{2}\left(\us{0}\us{2}\right) $$
The resulting cubic form is:
$$ N(\A{u}) = \A{u}\conj{\A{u}} = \A{1}\left(\us{0} \left(\us{1}\right)^{2} + \us{0} \left(\us{2}\right)^{2}\right) $$
The multiplicative inverse when $N(\A{x}) \ne 0$ is:
$$\A{x}^{-1} = \frac{\conj{\A{x}}}{N(\A{x})}$$
Matrix Representation
The $3$-plex number $\A{u}$ in diagonal basis has the following matrix representation:
We can verify that this corresponds to the expected multiplication:
Basis Conversion
The matrix representation $\lmat{\A{x}}$ admits the following decomposition:
$$ \begin{align*} \lmat{\A{x}} &= \A{P} \, \A{D}(\A{x}) \, \A{P}^{-1} \\ \\ \lmat{\A{x}} &= \begin{bmatrix} \xs{0}& \xs{2}& \xs{1} \\ \xs{1}& \xs{0}& \xs{2} \\ \xs{2}& \xs{1}& \xs{0} \end{bmatrix}\\ \\ \A{D}(\A{x}) &= \begin{bmatrix} \xs{0} + \xs{1} + \xs{2} & 0 & 0 \\ 0 & \frac{1}{2}\left(2\xs{0} - \xs{1} - \xs{2}\right) & -\frac{\sqrt{3}}{2}\left(\xs{1} - \xs{2}\right) \\ 0 & \frac{\sqrt{3}}{2}\left(\xs{1} - \xs{2}\right) & \frac{1}{2}\left(2\xs{0} - \xs{1} - \xs{2}\right) \end{bmatrix}\\ \\ \A{P} &= \begin{bmatrix} 1 & 1 & 0 \\ 1 & -\frac{1}{2} & \frac{\sqrt{3}}{2} \\ 1 & -\frac{1}{2} & -\frac{\sqrt{3}}{2} \end{bmatrix}\\ \end{align*} $$Consequently, it is possible to use $\A{P}$ to convert between standard and diagonal basis.
A $3$-plex number $\A{x}$ in standard basis can be written in diagonal basis as:
$$ \A{x} = \es{0}\xs{0} + \es{1}\xs{1} + \es{2}\xs{2} = \fs{0}\left(\xs{0} + \xs{1} + \xs{2}\right) + \fs{1}\frac{1}{2}\left(2\xs{0} - \xs{1} - \xs{2}\right) + \fs{2}\frac{\sqrt{3}}{2}\left(\xs{1} - \xs{2}\right) $$
A $3$-plex number $\A{u}$ in diagonal basis can be written in standard basis as:
$$ \A{u} = \fs{0}\us{0} + \fs{1}\us{1} + \fs{2}\us{2} = \es{0}\frac{1}{3}(\us{0}+2\us{1}) + \es{1}\frac{1}{3}(\us{0}-\us{1}+\sqrt{3}\us{3}) + \es{2}\frac{1}{3}(\us{0}-\us{1}-\sqrt{3}\us{3}) $$
4-Plex Numbers
We move on to the $4$-plex numbers $Pl_{4}(\mathbb{R})$.
$$ Pl_{4} \cong \mathbb{R} \oplus \mathbb{C} \oplus \mathbb{R} $$
Standard Basis
The $4$-plex number $\A{x}$ can be written in the standard basis as:
$$ \A{x} = \es{0}\xs{0} + \es{1}\xs{1} + \es{2}\xs{2} + \es{3}\xs{3} $$
Multiplication
The construction is as follows:
$$ \begin{align*} \left(\es{1}\right)^0 &= \es{0} \\ \left(\es{1}\right)^1 &= \es{1} \\ \left(\es{1}\right)^2 &= \es{2} \\ \left(\es{1}\right)^3 &= \es{3} \\ \left(\es{1}\right)^4 &= \es{0} \\ &\vdots \\ \end{align*} $$Resulting in the multiplication table:
Which gives the multiplication operation:
$$ \begin{alignat}{2} \A{x}\A{y} &={} &&\left(\es{0}\xs{0} + \es{1}\xs{1} + \es{2}\xs{2} + \es{3}\xs{3}\right)\left(\es{0}\ys{0} + \es{1}\ys{1} + \es{2}\ys{2} + \es{3}\ys{3}\right) \\ &= && \es{0}\left(\xs{0}~ \ys{0}+ \xs{3}~ \ys{1}+ \xs{2}~ \ys{2}+ \xs{1}~ \ys{3}\right) + \\ & && \es{1}\left(\xs{1}~ \ys{0}+ \xs{0}~ \ys{1}+ \xs{3}~ \ys{2}+ \xs{2}~ \ys{3}\right) + \\ & && \es{2}\left(\xs{2}~ \ys{0}+ \xs{1}~ \ys{1}+ \xs{0}~ \ys{2}+ \xs{3}~ \ys{3}\right) + \\ & && \es{3}\left(\xs{3}~ \ys{0}+ \xs{2}~ \ys{1}+ \xs{1}~ \ys{2}+ \xs{0}~ \ys{3}\right) \end{alignat} $$
The multiplicative unit is:
$$ \A{1} = \es{0} $$
Conjugate and Quartic Form
The $4$-plex number $\A{x}$ has the following principal conjugations:
$$ \begin{align*} \conjs{0}{\A{x}} &= \es{0}\xs{0} + \es{1}\xs{1} + \es{2}\xs{2} + \es{3}\xs{3} \\ \conjs{1}{\A{x}} &= \es{0}\xs{0} + \es{1}i\xs{1} - \es{2}\xs{2} - \es{3}i\xs{3} \\ \conjs{2}{\A{x}} &= \es{0}\xs{0} - \es{1}\xs{1} + \es{2}\xs{2} - \es{3}\xs{3} \\ \conjs{3}{\A{x}} &= \es{0}\xs{0} - \es{1}i\xs{1} - \es{2}\xs{2} + \es{3}i\xs{3} \\ \end{align*} $$The resulting conjugate is:
$$ \begin{alignat}{2} \conj{\A{x}} &={} &&\conjs{1}{\A{x}} \; \conjs{2}{\A{x}} \; \conjs{3}{\A{x}} = \\ &= &&\es{0}\left(\left(x^{0}\right)^{3} - x^{0} \left(x^{2}\right)^{2} + \left(x^{1}\right)^{2} x^{2} + x^{2} \left(x^{3}\right)^{2} - 2 x^{0} x^{1} x^{3}\right) -{} \\ & &&\es{1}\left(\left(x^{3}\right)^{3} + \left(x^{0}\right)^{2} x^{1} - \left(x^{1}\right)^{2} x^{3} + x^{1} \left(x^{2}\right)^{2} - 2 x^{0} x^{2} x^{3} \right) +{} \\ & &&\es{2}\left(\left(x^{2}\right)^{3} - \left(x^{0}\right)^{2} x^{2} + x^{0} \left(x^{1}\right)^{2} + x^{0} \left(x^{3}\right)^{2} - 2 x^{1} x^{2} x^{3}\right) -{} \\ & &&\es{3}\left(\left(x^{1}\right)^{3} + \left(x^{0}\right)^{2} x^{3} - x^{1} \left(x^{3}\right)^{2} + \left(x^{2}\right)^{2} x^{3} - 2 x^{0} x^{1} x^{2} \right) \\ \end{alignat} $$The resulting quartic form is:
$$ N(\A{x}) = \A{x}\conj{\A{x}} = \A{1}\left(\left(x^{0} + x^{1} + x^{2} + x^{3}\right) \left(x^{0} - x^{1} + x^{2} - x^{3}\right) \left(\left(x^{0}\right)^{2} - 2 x^{0} x^{2} + \left(x^{1}\right)^{2} - 2 x^{1} x^{3} + \left(x^{2}\right)^{2} + \left(x^{3}\right)^{2}\right)\right) $$
The multiplicative inverse when $N(\A{x}) \ne 0$ is:
$$\A{x}^{-1} = \frac{\conj{\A{x}}}{N(\A{x})}$$
Matrix Representation
The $4$-plex number $\A{x}$ in standard basis has the following matrix representation:
We can verify that this corresponds to the expected multiplication:
Diagonal Basis
The $4$-plex number $\A{u}$ can be written in the diagonal basis as:
$$ \A{u} = \fs{0}\us{0} + \fs{1}\us{1} + \fs{2}\us{2} + \fs{3}\us{3} $$
Multiplication
The construction is as follows:
$$ \begin{align*} \fs{0} &= \frac{1}{4} (\es{0} + \es{1} + \es{2} + \es{3}) \\ \fs{1} &= \frac{1}{2} (\es{0} - \es{2}) \\ \fs{2} &= \frac{1}{2} (\es{1} - \es{3}) \\ \fs{3} &= \frac{1}{4} (\es{0} - \es{1} + \es{2} - \es{3}) \\ \end{align*} $$Resulting in the multiplication table:
Which gives the multiplication operation:
$$ \begin{alignat}{2} \A{u}\A{v} &={} &&\left(\fs{0}\us{0} + \fs{1}\us{1} + \fs{2}\us{2} + \fs{3}\us{3}\right)\left(\fs{0}\vs{0} + \fs{1}\vs{1} + \fs{2}\vs{2} + \fs{3}\vs{3}\right) \\ &= && \fs{0}\left(\us{0}~ \vs{0}\right) + \\ & && \fs{1}\left(\us{1}~ \vs{1}- \us{2}~ \vs{2}\right) + \\ & && \fs{2}\left(\us{2}~ \vs{1}+ \us{1}~ \vs{2}\right) + \\ & && \fs{3}\left(\us{3}~ \vs{3}\right) + \\ \end{alignat} $$The multiplicative unit is:
$$ \A{1} = \fs{0} + \fs{1} + \fs{3} $$
Conjugate and Quartic Form
The $4$-plex number $\A{u}$ has the following principal conjugations:
$$ \begin{align*} \conjs{0}{\A{u}} &= \fs{0}\us{0} + \fs{1}\us{1} + \fs{2}\us{2} + \fs{3}\us{3} \\ \conjs{1}{\A{u}} &= \fs{0}\left(\us{1} + i\us{2}\right) + \fs{1}\frac{1}{2}\left(\us{0} + \us{3}\right) + \fs{2}\frac{i}{2}\left(\us{0} - \us{3}\right) + \fs{3}\left(\us{1} - i\us{2}\right) \\ \conjs{2}{\A{u}} &= \fs{0}\us{3} + \fs{1}\us{1} - \fs{2}\us{2} + \fs{3}\us{0} \\ \conjs{3}{\A{u}} &= \fs{0}\left(\us{1} - i\us{2}\right) + \fs{1}\frac{1}{2}\left(\us{0} + \us{3}\right) - \fs{2}\frac{i}{2}\left(\us{0} - \us{3}\right) + \fs{3}\left(\us{1} + i\us{2}\right) \\ \end{align*} $$The resulting conjugate is:
$$ \conj{\A{u}} = \conjs{1}{\A{u}} \; \conjs{2}{\A{u}} \; \conjs{3}{\A{u}} = \fs{0}\left(\left(\us{1}\right)^{2}\us{3} + \left(\us{2}\right)^{2}\us{3}\right) + \fs{1}\left(\us{0}\us{1}\us{3}\right) - \fs{2}\left(\us{0}\us{2}\us{3}\right) + \fs{3}\left(\us{0}\left(\us{1}\right)^{2} + \us{0}\left(\us{2}\right)^{2}\right) $$The resulting quartic form is:
$$ N(\A{u}) = \A{u}\conj{\A{u}} = \A{1}\left(\us{0}\left(\us{1}\right)^{2}\us{3} + \us{0}\left(\us{2}\right)^{2}\us{3}\right) $$
The multiplicative inverse when $N(\A{x}) \ne 0$ is:
$$\A{x}^{-1} = \frac{\conj{\A{x}}}{N(\A{x})}$$
Matrix Representation
The $4$-plex number $\A{u}$ in diagonal basis has the following matrix representation:
We can verify that this corresponds to the expected multiplication:
Basis Conversion
The matrix representation $\lmat{\A{x}}$ admits the following decomposition:
$$ \begin{align*} \lmat{\A{x}} &= \A{P} \, \A{D}(\A{x}) \, \A{P}^{-1} \\ \\ \lmat{\A{x}} &= \begin{bmatrix} \xs{0}& \xs{3}& \xs{2}& \xs{1} \\ \xs{1}& \xs{0}& \xs{3}& \xs{2} \\ \xs{2}& \xs{1}& \xs{0}& \xs{3} \\ \xs{3}& \xs{2}& \xs{1}& \xs{0} \end{bmatrix}\\ \\ \A{D}(\A{x}) &= \begin{bmatrix} \xs{0} + \xs{1} + \xs{2} + \xs{3} & 0 & 0 & 0 \\ 0 & \xs{0} - \xs{2} & -\xs{1} + \xs{3} & 0 \\ 0 & \xs{1} - \xs{3} & \xs{0} - \xs{2} & 0 \\ 0 & 0 & 0 & \xs{0} - \xs{1} + \xs{2} - \xs{3} \end{bmatrix}\\ \\ \A{P} &= \begin{bmatrix} 1 & 1 & 0 & 1\\ 1 & 0 & 1 & -1\\ 1 & -1 & 0 & 1\\ 1 & 0 & -1 & -1 \end{bmatrix}\\ \end{align*} $$Consequently, it is possible to use $\A{P}$ to convert between standard and diagonal basis.
A $4$-plex number $\A{x}$ in standard basis can be written in diagonal basis as:
$$ \begin{alignat}{2} \A{x} &={} &&\es{0}\xs{0} + \es{1}\xs{1} + \es{2}\xs{2} + \es{3}\xs{3} \\ &= &&\fs{0}\left(x^{0} + x^{1} + x^{2} + x^{3}\right) + \\ & &&\fs{1}\left(x^{0} - x^{2}\right) + \\ & &&\fs{2}\left(x^{1} - x^{3}\right) + \\ & &&\fs{3}\left(x^{0} - x^{1} + x^{2} - x^{3}\right) \end{alignat} $$A $4$-plex number $\A{u}$ in diagonal basis can be written in standard basis as:
$$ \begin{alignat}{2} \A{u} &={} &&\fs{0}\us{0} + \fs{1}\us{1} + \fs{2}\us{2} + \fs{3}\us{3} \\ &= &&\es{0}\frac{1}{4}(\us{0}+2\us{1}+\us{3}) +{} \\ & &&\es{1}\frac{1}{4}(\us{0}+2\us{2}-\us{3}) +{} \\ & &&\es{2}\frac{1}{4}(\us{0}-2\us{1}+\us{3}) +{} \\ & &&\es{3}\frac{1}{4}(\us{0}-2\us{2}-\us{3}) \end{alignat} $$n-Plex Numbers
Finally, let us consider the $(n+1)$-plex numbers $Pl_{n+1}(\mathbb{R})$.
$$ \begin{align*} Pl_{n+1} \cong \begin{cases} \mathbb{R} \oplus \left(\bigoplus_{i = 0}^{m}\mathbb{C}\right) & {\text{if }} n+1 {\text{ odd}}, \\ \mathbb{R} \oplus \left(\bigoplus_{i = 0}^{m}\mathbb{C}\right) \oplus \mathbb{R} & {\text{if }} n+1 {\text{ even}}. \end{cases} \end{align*} $$Where $m = \lfloor\frac{n}{2}\rfloor$.
Standard Basis
The $(n+1)$-plex numbers $\A{x}$ can be written in the standard basis as:
$$ \A{x} = \es{0}\xs{0} + \es{1}\xs{1} + \dots + \es{n}\xs{n} $$
Multiplication
The construction is as follows:
$$ \left(\es{1}\right)^k = \es{(k \bmod n)} $$
Resulting in the multiplication table:
Or alternatively:
$$ \es{i}\es{j} = \es{\left(\left(i+j\right) \bmod n\right)} $$
The multiplicative unit is:
$$ \A{1} = \es{0} $$
Conjugate and N Form
The $(n+1)$-plex number $\A{x}$ has the following principal conjugations:
$$ \conjs{k}{\A{x}} = \sum_{j=0}^{n} \left(\zeta^{k}\right)^{j}\xs{j}\es{j} $$The resulting conjugate is:
$$ \conj{\A{x}} = \prod_{k=1}^{n} \conjs{k}{\A{x}} $$The resulting N form is:
$$ N(\A{x}) = \A{x}\conj{\A{x}} $$
The multiplicative inverse when $N(\A{x}) \ne 0$ is:
$$\A{x}^{-1} = \frac{\conj{\A{x}}}{N(\A{x})}$$
Matrix Representation
The $(n+1)$-plex number $\A{x}$ in standard basis has the following matrix representation:
$$ \lmat{\A{x}} = \begin{bmatrix} \xs{0} & \xs{n} & \cdots & \xs{2} & \xs{1} \\ \xs{1} & \xs{0} & \cdots & \xs{3} & \xs{2} \\ \vdots & \vdots & \ddots & \vdots & \vdots \\ \xs{n-1} & \xs{n-2} & \cdots & \xs{0} & \xs{n} \\ \xs{n} & \xs{n-1} & \cdots & \xs{1} & \xs{0} \end{bmatrix} $$Or alternatively:
$$ \Xs{j}{i} = \xs{\left(\left(i-j\right) \bmod n\right)} $$
We can verify that this corresponds to the expected multiplication:
$$ \begin{bmatrix} \xs{0} & \xs{n} & \cdots & \xs{2} & \xs{1} \\ \xs{1} & \xs{0} & \cdots & \xs{3} & \xs{2} \\ \vdots & \vdots & \ddots & \vdots & \vdots \\ \xs{n-1} & \xs{n-2} & \cdots & \xs{0} & \xs{n} \\ \xs{n} & \xs{n-1} & \cdots & \xs{1} & \xs{0} \end{bmatrix} \begin{bmatrix} \ys{0} \\ \ys{1} \\ \vdots \\ \ys{n-1} \\ \ys{n} \end{bmatrix} = \begin{bmatrix} \xs{0}\ys{0} + \xs{n}\ys{1} + \dots + \xs{2}\ys{n-1} + \xs{1}\ys{n} \\ \xs{1}\ys{0} + \xs{0}\ys{1} + \dots + \xs{3}\ys{n-1} + \xs{2}\ys{n} \\ \vdots \\ \xs{n-1}\ys{0} + \xs{n-2}\ys{1} + \dots + \xs{0}\ys{n-1} + \xs{n}\ys{n} \\ \xs{n}\ys{0} + \xs{n-1}\ys{1} + \dots + \xs{1}\ys{n-1} + \xs{0}\ys{n} \end{bmatrix} $$Or alternatively:
$$ \Xs{j}{i}\ys{j} = \sum_{j=0}^{n}{\xs{\left(\left(i-j\right) \bmod n\right)}\ys{j}} $$
Diagonal Basis
The $(n+1)$-plex number $\A{u}$ can be written in the diagonal basis as:
$$ \A{u} = \fs{0}\us{0} + \fs{1}\us{1} + \dots + \fs{n}\us{n} $$
Multiplication
Resulting in the multiplication table:
If $n+1$ is odd:
If $n+1$ is even:
The multiplicative unit is:
$$ \begin{align*} \A{1} = \begin{cases} \fs{0} + \sum_{k=0}^{m}{\fs{2k+1}} & {\text{if }} n+1 {\text{ odd}}, \\ \fs{0} + \sum_{k=0}^{m}{\fs{2k+1}} + \fs{n} & {\text{if }} n+1 {\text{ even}}. \end{cases} \end{align*} $$Matrix Representation
The $(n+1)$-plex number $\A{u}$ in diagonal basis has the following matrix representation:
$$ \lmat{\A{u}} = \begin{bmatrix} \us{0} & 0 & 0 & \cdots & 0 & 0 \\ 0 & \us{1} & -\us{2} & \cdots & 0 & 0 \\ 0 & \us{2} & \us{1} & \cdots & 0 & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots & \vdots \\ 0 & 0 & 0 & \cdots & \us{n-1} & -\us{n} \\ 0 & 0 & 0 & \cdots & \us{n} & \us{n-1} \end{bmatrix} $$We can verify that this corresponds to the expected multiplication:
$$ \begin{bmatrix} \us{0} & 0 & 0 & \cdots & 0 & 0 \\ 0 & \us{1} & -\us{2} & \cdots & 0 & 0 \\ 0 & \us{2} & \us{1} & \cdots & 0 & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots & \vdots \\ 0 & 0 & 0 & \cdots & \us{n-1} & -\us{n} \\ 0 & 0 & 0 & \cdots & \us{n} & \us{n-1} \end{bmatrix} \begin{bmatrix} \vs{0} \\ \vs{1} \\ \vs{2} \\ \vdots \\ \vs{n-1} \\ \vs{n} \end{bmatrix} = \begin{bmatrix} \us{0}\vs{0} \\ \us{1}\vs{1} - \us{2}\ys{2} \\ \us{2}\vs{1} + \us{1}\ys{2} \\ \vdots \\ \us{n-1}\vs{n-1} - \us{n}\vs{n} \\ \us{n}\vs{n-1} + \us{n-1}\ys{n} \end{bmatrix} $$Basis Conversion
Congratulations, you have made it to the interesting part! 🎉
The matrix representation $\lmat{\A{x}}$ admits the following decomposition:
$$ \begin{align*} \lmat{\A{x}} &= \A{P} \, \A{D}(\A{x}) \, \A{P}^{-1} \\ \\ \lmat{\A{x}} &= \begin{bmatrix} \xs{0} & \xs{n} & \cdots & \xs{2} & \xs{1} \\ \xs{1} & \xs{0} & \cdots & \xs{3} & \xs{2} \\ \vdots & \vdots & \ddots & \vdots & \vdots \\ \xs{n-1} & \xs{n-2} & \cdots & \xs{0} & \xs{n} \\ \xs{n} & \xs{n-1} & \cdots & \xs{1} & \xs{0} \end{bmatrix} \end{align*} $$However, the question is how do we compute $\A{P}$ in general? This is where the eigenvalue decomposition comes into play.
It is easy to verify that the following are eigenvalues of the matrix $\lmat{\A{x}}$:
$$ \lambda_{k}\left(\A{x}\right) = \sum_{j=0}^{n} \left(\zeta^{k}\right)^{j} \xs{j} $$
Furthermore, we can similarly find the corresponding eigenvectors.
$$ \A{v}_{\lambda_{k}} = \begin{bmatrix} \left(\bar{\zeta}^{k}\right)^{0} \\ \left(\bar{\zeta}^{k}\right)^{1} \\ \left(\bar{\zeta}^{k}\right)^{2} \\ \vdots \\ \left(\bar{\zeta}^{k}\right)^{n} \end{bmatrix} $$Where $\zeta^{k}$ are the $n$-th roots of unity, and $\bar{\zeta}^{k}$ denotes complex conjugation.
Consequently, the matrix $\lmat{\A{x}}$ has the following complex diagonal form:
$$ \begin{align*} \lmat{\A{x}} &= \A{P} \, \A{D}(\A{x}) \, \A{P}^{-1} \\ \\ \A{D}(\A{x}) &= \begin{bmatrix} \lambda_{0}\left(\A{x}\right) & 0 & \cdots & 0 \\ 0 & \lambda_{1}\left(\A{x}\right) & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & \lambda_{n}\left(\A{x}\right) \end{bmatrix}\\ \\ \A{P} &= \begin{bmatrix} \left(\bar{\zeta}^{0}\right)^{0} & \left(\bar{\zeta}^{1}\right)^{0} & \cdots & \left(\bar{\zeta}^{n}\right)^{0} \\ \left(\bar{\zeta}^{0}\right)^{1} & \left(\bar{\zeta}^{1}\right)^{1} & \cdots & \left(\bar{\zeta}^{n}\right)^{1} \\ \vdots & \vdots & \ddots & \vdots \\ \left(\bar{\zeta}^{0}\right)^{n} & \left(\bar{\zeta}^{1}\right)^{n} & \cdots & \left(\bar{\zeta}^{n}\right)^{n} \end{bmatrix}\\ \end{align*} $$Or alternatively:
$$ \begin{align*} D_{j}^{i} &= \lambda_{j}\left(\A{x}\right) \; \delta_{j}^{i} \\ P_{j}^{i} &= \left(\bar{\zeta}^{j}\right)^{i} \end{align*} $$Now for the nice part: Notice that $P$ is a Vandermonde matrix! That means we have "nice" formulas for the determinant $\det(\A{P})$.
$$ \det(\A{P}) = \prod_{0 \leq i \lt j \leq n}(\bar{\zeta}^{i} - \bar{\zeta}^{j}) $$The inverse takes a particularly simple form:
$$ \A{P}^{-1} = \frac{1}{n} \begin{bmatrix} \left(\zeta^{0}\right)^{0} & \left(\zeta^{1}\right)^{0} & \cdots & \left(\zeta^{n}\right)^{0} \\ \left(\zeta^{0}\right)^{1} & \left(\zeta^{1}\right)^{1} & \cdots & \left(\zeta^{n}\right)^{1} \\ \vdots & \vdots & \ddots & \vdots \\ \left(\zeta^{0}\right)^{n} & \left(\zeta^{1}\right)^{n} & \cdots & \left(\zeta^{n}\right)^{n} \end{bmatrix} $$However, there is still a problem: As the name suggests, the complex diagonal form may contain complex numbers. We would prefer to work over the reals. For that purpose we need to convert from the complex diagonal form to the real diagonal form which contains real 2-by-2 blocks in place of complex conjugate pairs along the diagonal. This may be done using cdf2rdf.