Number Systems
$$ \newcommand{\placeholder}{\ast} \newcommand{\N}{n} \newcommand{\K}{k} \newcommand{\H}[1]{h_{#1}} \newcommand{\cosk}[1]{\operatorname{\mathfrak{c}_{#1}}} \newcommand{\sink}[1]{\operatorname{\mathfrak{s}_{#1}}} \newcommand{\tank}[1]{\operatorname{\mathfrak{t}_{#1}}} $$This page documents a few interesting number systems.
Preliminaries
The unified treatments below make use of generalized trigonometric functions.
Complex Number Family
Initially, we consider a few select members of the complex number family. In the process, we highlight parellels between them. Subsequently, we provide a unified perspective.
Individual Members
Let us consider the complex numbers, and two of their close relatives. Each corresponding to one choice from $\{-1, 0, +1\}$.
Complex Numbers
Cartesian Forms
Numbers of the form: $$z = a + ib$$ where:
- $i^{2}= -1$
Operations
Given $z = a + ib$ we have:
Addition
$$\small \begin{split}z_0 + z_1 = (a_0 + i b_0) + (a_1 + i b_1) \\= (a_0 + a_1) + i(b_0 + b_1)\end{split}$$Additive Inverse
$$-z = -a - ib$$Multiplication
$$\small \begin{split}z_0 z_1 = (a_0 + i b_0) (a_1 + i b_1) \\= (a_0 a_1 - b_0 b_1) + i(a_0 b_1 + b_0 a_1)\end{split}$$Conjugate
$$\overline{z} = a - ib$$Quadratic Form
$$|z|^2 = z\overline{z} = a^2 + b^2$$Multiplicative Inverse
$$z^{-1} = \frac{\overline{z}}{z\overline{z}} = \frac{\overline{z}}{|z|^2}$$Polar/Exponential Forms
Substituting $i\theta$ for $x$ in $e^{x}$: $$e^{i\theta} = \cos(\theta) + i\sin(\theta)$$ which motivates: $$z = r(\cos(\theta) + i\sin(\theta)) = re^{i\theta}$$
Operations
Given $z = r e^{i \theta}$ we have:
Multiplication
$$\small z_0 z_1 = (r_0 e^{i \theta_0}) (r_1 e^{i \theta_1}) = (r_0 r_1) e^{i (\theta_0+ \theta_1)}$$Conjugate
$$\overline{z} = r e^{i (-\theta)}$$Quadratic Form
$$|z|^2 = z\overline{z} = r^2$$Multiplicative Inverse
$$z^{-1} = \frac{\overline{z}}{|z|^2} = \frac{1}{r} e^{i(-\theta)}$$Conversions
Given $z = re^{i\theta}$ we obtain: $$ \begin{align*} a &= r\cos(\theta)\\\\ b &= r\sin(\theta) \end{align*} $$
Given $z = a + ib$ we obtain: $$ \begin{align*} r &= \sqrt{a^2 + b^2}\\\\ \theta &= \operatorname{atan2}(b,a) \end{align*} $$
Operations
Exponential
Using $e^{x+y} = e^{x} e^{y}$: $$ e^{z} = e^{a + ib} = e^{a} e^{ib} $$
Logarithm
Using $\ln(x y) = \ln(x) + \ln(y)$: $$ \ln(z) = \ln(re^{i\theta}) = \ln(r) + i\theta $$
Exponentiation
$$ z_0^{z_1} = e^{\ln(z_0) z_1} $$
Plots
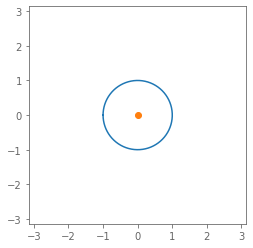
All $z = a + ib$ with:
- $|z|^2 = -1$ ($\varnothing$)
- $|z|^2 = \phantom{+}0$ (orange)
- $|z|^2 = +1$ (blue)
Dual Numbers
Cartesian Forms
Numbers of the form: $$z = a + \epsilon b$$ where:
- $\epsilon^{2}= 0$
Operations
Given $z = a + \epsilon b$ we have:
Addition
$$\small \begin{split}z_0 + z_1 = (a_0 + \epsilon b_0) + (a_1 + \epsilon b_1) \\= (a_0 + a_1) + \epsilon (b_0 + b_1)\end{split}$$Additive Inverse
$$-z = -a - \epsilon b$$Multiplication
$$\small \begin{split}z_0 z_1 = (a_0 + \epsilon b_0) (a_1 + \epsilon b_1) \\= (a_0 a_1) + \epsilon (a_0 b_1 + b_0 a_1)\end{split}$$Conjugate
$$\overline{z} = a - \epsilon b$$Quadratic Form
$$|z|^2 = z\overline{z} = a^2$$Multiplicative Inverse
$$z^{-1} = \frac{\overline{z}}{z\overline{z}} = \frac{\overline{z}}{|z|^2}$$Polar/Exponential Forms
Substituting $\epsilon\theta$ for $x$ in $e^{x}$: $$e^{\epsilon\theta} = 1 + \epsilon\theta$$ which motivates: $$z = r(1 + \epsilon\theta) = re^{\epsilon\theta}$$
Operations
Given $z = r e^{\epsilon \theta}$ we have:
Multiplication
$$\small z_0 z_1 = (r_0 e^{\epsilon \theta_0}) (r_1 e^{\epsilon \theta_1}) = (r_0 r_1) e^{\epsilon (\theta_0 + \theta_1)}$$Conjugate
$$\overline{z} = r e^{\epsilon (-\theta)}$$Quadratic Form
$$|z|^2 = z\overline{z} = r^2$$Multiplicative Inverse
$$z^{-1} = \frac{\overline{z}}{|z|^2} = \frac{1}{r} e^{\epsilon (-\theta)}$$Conversions
Given $z = re^{\epsilon \theta}$ we obtain: $$ \begin{align*} a &= r\\\\ b &= r\theta \end{align*} $$
Given $z = a + \epsilon b$ we obtain: $$ \begin{align*} r &= \sqrt{a^2}\\\\ \theta &= \frac{b}{a} \end{align*} $$
Operations
Exponential
Using $e^{x+y} = e^{x} e^{y}$: $$ e^{z} = e^{a + \epsilon b} = e^{a} e^{\epsilon b} $$
Logarithm
Using $\ln(x y) = \ln(x) + \ln(y)$: $$ \ln(z) = \ln(re^{\epsilon\theta}) = \ln(r) + \epsilon\theta $$
Exponentiation
$$ z_0^{z_1} = e^{\ln(z_0) z_1} $$
Plots
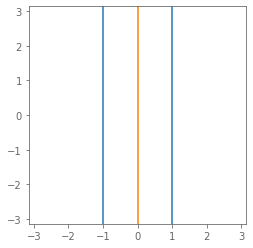
All $z = a + \epsilon b$ with:
- $|z|^2 = -1$ ($\varnothing$)
- $|z|^2 = \phantom{+}0$ (orange)
- $|z|^2 = +1$ (blue)
Split-Complex Numbers
Cartesian Forms
Numbers of the form: $$z = a + jb$$ where:
- $j^{2}= +1$
Operations
Given $z = a + jb$ we have:
Addition
$$\small \begin{split}z_0 + z_1 = (a_0 + j b_0) + (a_1 + j b_1) \\= (a_0 + a_1) + j(b_0 + b_1)\end{split}$$Additive Inverse
$$-z = -a - jb$$Multiplication
$$\small \begin{split}z_0 z_1 = (a_0 + j b_0) (a_1 + j b_1) \\= (a_0 a_1 + b_0 b_1) + j(a_0 b_1 + b_0 a_1)\end{split}$$Conjugate
$$\overline{z} = a - jb$$Quadratic Form
$$|z|^2 = z\overline{z} = a^2 - b^2$$Multiplicative Inverse
$$z^{-1} = \frac{\overline{z}}{z\overline{z}} = \frac{\overline{z}}{|z|^2}$$Polar/Exponential Forms
Substituting $j\theta$ for $x$ in $e^{x}$: $$e^{j\theta} = \cosh(\theta) + j\sinh(\theta)$$ which motivates: $$z = r(\cosh(\theta) + j\sinh(\theta)) = re^{j\theta}$$
Operations
Given $z = r e^{j \theta}$ we have:
Multiplication
$$\small z_0 z_1 = (r_0 e^{j \theta_0}) (r_1 e^{j \theta_1}) = (r_0 r_1) e^{j (\theta_0 + \theta_1)}$$Conjugate
$$\overline{z} = r e^{j (-\theta)}$$Quadratic Form
$$|z|^2 = z\overline{z} = r^2$$Multiplicative Inverse
$$z^{-1} = \frac{\overline{z}}{|z|^2} = \frac{1}{r} e^{j (-\theta)}$$Conversions
Given $z = re^{j\theta}$ we obtain: $$ \begin{align*} a &= r\cosh(\theta)\\\\ b &= r\sinh(\theta) \end{align*} $$
Given $z = a + jb$ we obtain: $$ \begin{align*} r &= \sqrt{a^2 - b^2}\\\\ \theta &= \tanh^{-1}(\frac{b}{a}) \end{align*} $$
Operations
Exponential
Using $e^{x+y} = e^{x} e^{y}$: $$ e^{z} = e^{a + jb} = e^{a} e^{jb} $$
Logarithm
Using $\ln(x y) = \ln(x) + \ln(y)$: $$ \ln(z) = \ln(re^{j\theta}) = \ln(r) + j\theta $$
Exponentiation
$$ z_0^{z_1} = e^{\ln(z_0) z_1} $$
Plots
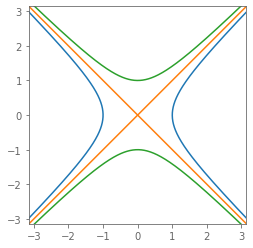
All $z = a + jb$ with:
- $|z|^2 = -1$ (green)
- $|z|^2 = \phantom{+}0$ (orange)
- $|z|^2 = +1$ (blue)
Unified Family
$\newcommand{\K}{k}$The similarities in the number systems above suggest a possible unification as follows.
Unified Complex Numbers
Cartesian Forms
Numbers of the form: $$z = a + \kappa b$$ where:
- $\kappa^{2}= -\K$
Operations
Given $z_{\placeholder} = a_{\placeholder} + \kappa b_{\placeholder}$ we have:
Addition
$$\small \begin{split}z_0 + z_1 = (a_0 + \kappa b_0) + (a_1 + \kappa b_1) \\= (a_0 + a_1) + \kappa (b_0 + b_1)\end{split}$$Additive Inverse
$$-z = -a - \kappa b$$Multiplication
$$\small \begin{split}z_0 z_1 = (a_0 + \kappa b_0) (a_1 + \kappa b_1) \\= (a_0 a_1 - \K b_0 b_1) + \kappa (a_0 b_1 + b_0 a_1)\end{split}$$Conjugate
$$\overline{z} = a - \kappa b$$Quadratic Form
$$|z|^2 = z\overline{z} = a^2 + \K b^2$$Multiplicative Inverse
$$z^{-1} = \frac{\overline{z}}{z\overline{z}} = \frac{\overline{z}}{|z|^2}$$Polar/Exponential Forms
Substituting $\kappa\theta$ for $x$ in $e^{x}$: $$e^{\kappa\theta} = \mathfrak{c}_{\K}(\theta) + \kappa\mathfrak{s}_{\K}(\theta)$$ which motivates: $$z = r(\mathfrak{c}_{\K}(\theta) + \kappa\mathfrak{s}_{\K}(\theta)) = re^{\kappa\theta}$$
Operations
Given $z_{\placeholder} = r_{\placeholder} e^{\kappa \theta_{\placeholder}}$ we have:
Multiplication
$$z_0 z_1 = (r_0 e^{\kappa \theta_0}) (r_1 e^{\kappa \theta_1}) = (r_0 r_1) e^{\kappa (\theta_0 + \theta_1)}$$Conjugate
$$\overline{z} = r e^{\kappa (-\theta)}$$Quadratic Form
$$|z|^2 = z\overline{z} = r^2$$Multiplicative Inverse
$$z^{-1} = \frac{\overline{z}}{|z|^2} = \frac{1}{r} e^{\kappa (-\theta)}$$Conversions
Given $z = re^{\kappa\theta}$ we obtain: $$ \begin{align*} a &= r\mathfrak{c}_{\K}(\theta)\\\\ b &= r\mathfrak{s}_{\K}(\theta) \end{align*} $$
Given $z = a + \kappa b$ we obtain: $$ \begin{align*} r &= \sqrt{a^2 + \K b^2}\\\\ \theta &= \mathfrak{t}_{\K}^{-1}(\frac{b}{a}) \end{align*} $$
Operations
Exponential
Using $e^{x+y} = e^{x} e^{y}$: $$ e^{z} = e^{a + \kappa b} = e^{a} e^{\kappa b} $$
Logarithm
Using $\ln(x y) = \ln(x) + \ln(y)$: $$ \ln(z) = \ln(re^{\kappa\theta}) = \ln(r) + \kappa\theta $$
Exponentiation
$$ z_0^{z_1} = e^{\ln(z_0) z_1} $$
Quaternion Family
Initially, we consider a few select members of the quaternion family. In the process, we highlight parellels between them. Subsequently, we provide a unified perspective.
Individual Members
Let us consider the quaternions, and eight of their close relatives. Each corresponding to two choices from $\{-1, 0, +1\}$.
Quaternions
Cartesian Forms
Numbers of the form: $$z = a + ib + jc + kd$$ where:
- $i^{2} = -1$
- $j^{2} = -1$
- $ij = k = -ji$
Semi-Quaternions
Cartesian Forms
Numbers of the form: $$z = a + ib + jc + kd$$ where:
- $i^{2} = -1$
- $j^{2} = 0$
- $ij = k = -ji$
Split-Quaternions
Cartesian Forms
Numbers of the form: $$z = a + ib + jc + kd$$ where:
- $i^{2} = -1$
- $j^{2} = +1$
- $ij = k = -ji$
Semi-Quaternions
Cartesian Forms
Numbers of the form: $$z = a + ib + jc + kd$$ where:
- $i^{2}= 0$
- $j^{2}= -1$
- $ij = k = -ji$
Quarter-Quaternions
Cartesian Forms
Numbers of the form: $$z = a + ib + jc + kd$$ where:
- $i^{2}= 0$
- $j^{2}= 0$
- $ij = k = -ji$
Split-Semi-Quaternions
Cartesian Forms
Numbers of the form: $$z = a + ib + jc + kd$$ where:
- $i^{2}= 0$
- $j^{2}= +1$
- $ij = k = -ji$
Split-Quaternions
Cartesian Forms
Numbers of the form: $$z = a + ib + jc + kd$$ where:
- $i^{2}= +1$
- $j^{2}= -1$
- $ij = k = -ji$
Split-Semi-Quaternions
Cartesian Forms
Numbers of the form: $$z = a + ib + jc + kd$$ where:
- $i^{2}= +1$
- $j^{2}= 0$
- $ij = k = -ji$
Split-Quaternions
Cartesian Forms
Numbers of the form: $$z = a + ib + jc + kd$$ where:
- $i^{2}= +1$
- $j^{2}= +1$
- $ij = k = -ji$
Thankfully, upon closer inspection, we discover that some of these family members are essentially the same except in disguise (i.e. they are isomorphic/equivalent up to a renaming of $i, j, k$).
In the interest of brevity, we proceed directly with the unified family, which covers all the possible cases.
Unified Family
As with the complex number family, we can also unify quaternion family.
Unified Quaternions
Cartesian Form
Numbers of the form: $$z = a + ib + jc + kd$$ where:
- $i^{2}= -h_0$
- $j^{2}= -h_1$
- $ij = k = -ji$
Operations
Given $z_{\placeholder} = a_{\placeholder} + ib_{\placeholder} + jc_{\placeholder} + kd_{\placeholder}$ we have:
Addition
$$\small \begin{split}z_0 + z_1 = (a_0 + i b_0 + j c_0 + k d_0) + (a_1 + i b_1 + j c_1 + k d_1) \\= (a_0 + a_1) + i(b_0 + b_1) + j(c_0 + c_1) + k(d_0 + d_1)\end{split}$$Additive Inverse
$$-z = -a - ib - jc - kd$$Multiplication
$$\small \begin{alignat}{2} z_0 z_1 &=\; &&(a_0 + i b_0 + j c_0 + k d_0) (a_1 + i b_1 + j c_1 + k d_1) \\\\ &= &&\phantom{+ 1} (a_0 a_1 - h_0 b_0 b_1 - h_1 c_0 c_1 - h_0 h_1 d_0 d_1) \\\\ & &&+ i (a_0 b_1 + a_1 b_0 + h_1 c_0 d_1 - h_1 c_1 d_0) \\\\ & &&+ j (a_0 c_1 + a_1 c_0 - h_0 b_0 d_1 + h_0 b_1 d_0) \\\\ & &&+ k (a_0 d_1 + a_1 d_0 + b_0 c_1 - b_1 c_0) \end{alignat} $$Conjugate
$$\overline{z} = a - ib - jc - kd$$Quadratic Form
$$|z|^2 = z\overline{z} = a^2 + h_0 b^2 + h_1 c^2 + h_0 h_1 d^2$$Multiplicative Inverse
$$z^{-1} = \frac{\overline{z}}{z\overline{z}} = \frac{\overline{z}}{|z|^2}$$Real/Imaginary Parts
Alternatively, $z = a + ib + jc + kd$ can be rewritten as: $$ z = a + (ib' + jc' + kd')e = a + \hat{n} e $$ where $b' = \frac{b}{e},\; c' = \frac{c}{e},\; d' = \frac{d}{e}$.
With real part $a$ and imaginary part $\hat{n} e$. $$ \hat{n}^2 = -|\hat{n}|^2 = -\H0 {b'}^2 -\H1 {c'}^2 -\H0\H1 {d'}^2 $$
Note that two different $z_0, z_1$ need not share the same $\hat{n}$.
Polar/Exponential Forms
Substituting $\hat{n} \theta$ for $x$ in $e^{x}$: $$e^{\hat{n}\theta} = \cosk{\N}(\theta) + \hat{n}\sink{\N}(\theta)$$ where $\N = |\hat{n}|^2$ and $\hat{n}$ is imaginary: $$\hat{n} = i b' + j c' + k d'$$ which motivates: $$z = r(\cosk{\N}(\theta) + \hat{n}\sink{\N}(\theta)) = re^{\hat{n}\theta}$$
Operations
Given $z_{\placeholder} = r_{\placeholder} e^{\hat{n} \theta_{\placeholder}}$ we have:
Multiplication
$$z_0 z_1 = (r_0 e^{\hat{n} \theta_0}) (r_1 e^{\hat{n} \theta_1}) = (r_0 r_1) e^{\hat{n} (\theta_0 + \theta_1)}$$Conjugate
$$\overline{z} = r e^{\hat{n} (-\theta)}$$Quadratic Form
$$|z|^2 = z\overline{z} = r^2$$Multiplicative Inverse
$$z^{-1} = \frac{\overline{z}}{|z|^2} = \frac{1}{r} e^{\hat{n} (-\theta)}$$Conversions
Given $z = re^{\hat{n} \theta}$ we obtain: $$ \begin{align*} a &= r\cosk{\N}(\theta) \\\\ b &= r\sink{\N}(\theta) \end{align*} $$
Given $z = a + \hat{n} b$ we obtain: $$ \begin{align*} r &= \sqrt{a^2 + \N b^2}\\\\ \theta &= \tank{\N}^{-1}(\frac{b}{a}) \end{align*} $$
Operations
Exponential
Using $e^{x+y} = e^{x} e^{y}$: $$ e^{z} = e^{a + \hat{n} b} = e^{a} e^{\hat{n} b} $$
Logarithm
Using $\ln(x y) = \ln(x) + \ln(y)$: $$ \ln(z) = \ln(re^{\hat{n} \theta}) = \ln(r) + \hat{n} \theta $$
Exponentiation
$$ \begin{align*} z_0^{z_1} = e^{\ln(z_0)\, z_1} \\\\ ^{z_1}z_0 = e^{z_1 \ln(z_0)} \end{align*} $$